Ontolog Forum
UoM_Ontology_Standard (Reference) UML Model - draft
Editor: David Leal
This is the workspace for the drafting of the UoM_Ontology_Standard (Reference) UML Model
A strawman UML model based upon initial discussions
Introduction
This in an attempt to summarise part of the discussion so far. Very interesting threads about:
- the relationships between quantities and measurement methods;
- non-scalar quantities;
- dimensionless quantities, especially angle;
have not yet been addressed.
Sources
The principal sources for the strawman have been:
- the International Vocabulary of Metrology - Basic and General Concepts and Associated Terms (VIM) (http://www.bipm.org/en/publications/guides/vim.html);
- a UML model derived from VIM, with an extension for scales, developed by a team including NIST, which was supplied by Ed Barkmeyer;
- content of the e-mail discussion on [ uom-ontology-std ].
A strawman for quantity
A strawman UML diagram for "quantity" is: 
The differences between the Strawman and the original UML diagram supplied by Ed, include the following:
- The concept "quantity" has been split into generic quantity and particular quantity.
- The concept magnitude of quantity has been introduced.
- A quantity value does not necessarily reference a unit. This is not what the VIM says. There are a number of things which could be referenced, including a unit.
- The concept particular phenomenon body or substance has been introduced. This seems appropriate because quantities do not exist without something to possess them.
The UML diagram does not purport to be an ontology, but is an informal representation of the concepts related to "quantity" that have been discussed so far and their relationships.
The text associated with the UML objects shows an unsolved problem, as follows:
- Rockwell C hardness (150 kg) is shown as an example of generic quantity. It seems appropriate to include Rockwell C hardness (150 kg) as a generic quantity alongside thickness or radius, because it is something that can be measured for a particular solid object.
- Rockwell C hardness (150 kg) is shown as an example of kind of quantity. It seems appropriate to include Rockwell C hardness (150 kg) as a kind of quantity alongside length, because a measurement of Rockwell C hardness (150 kg) provides an expression of a magnitude of quantity that is within Rockwell C hardness (150 kg). Similarly a measurement of radius provides an expression of a magnitude of quantity that is within length.
The same would be true of mass.
Distinction between magnitude of quantity and quantity value
In the strawman UML diagram, quantity value is a data structure that expresses a magnitude of quantity. This is a valid interpretation of the VIM. With this interpretation, 5.34 m and 534 cm are two different instances of quantity value which express the same magnitude of quantity.
However, the clause that defines quantity value contains "NOTE 3 A quantity value can be presented in more than one way." This note implies a different terminology, but not a different model structure. Taking account of this note:
- magnitude of quantity in the strawman UML would be called quantity value;
- quantity value in the strawman UML would be called quantity presentation.
Discussion of Rockwell C hardness
It seems straightforward that Rockwell_C_hardness_(150kg) is a kind of quantity. Within this kind of quantity, the there is a magnitude of quantity that is expressed by the quantity value (55, Rockwell_C_hardness_(150_kg)). So far so good - this is consistent with the strawman UML model. Note that in this case the reference from the quantity value is not a unit but a measurement procedure.
The difficulty is the relationship between my_lump_of_hard_steel and the magnitude of quantity' that is expressed as (55, Rockwell_C_hardness_(150_kg)). One approach is to regard the magnitude of quantity as the class of objects that have the specified response the the measurement procedure. Hence in this case, the link between magnitude of quantity and particular phenomenon body or substance, which is labelled particular quantity, is classification.
The relationship is not always classification, because consider waterline length of a ship. If the ship Medway_Queen has a waterline length of 20 metres, then we have:
- the particular phenomenon body or substance that is the Medway_Queen;
- the magnitude of quantity thas is expressed by the quantity value (20, metre);
- the particular quantity relationship has_waterline_length between the two.
In this case, the particular quantity relationship is of a special type - has_waterline_length.
The relationship has_waterline_length is a shorthand for something quite complicated. There is a relationship has_extreme_waterline_point_pair between a ship and a point pair. Just as the magnitude of quantity that is expressed as (55, Rockwell_C_hardness_(150_kg)) can be regarded as a class with solid objects as members, the magnitude of quantity that is expressed as (20, metre) can be regarded as a class that has point pairs as members.
Hence for the ship there are two relationships: has_extreme_waterline_point_pair and classification, which are composed to give has_waterline_length. This seems to be a very common case, where the nature of the relationship between a physical object and a magnitude of quantity embodies a great deal of domain knowledge, and the kind of quantity is simple. For Rockwell hardness the relationship is simply classification, and the domain knowledge is embodied in the kind of quantity. The strawman UML model handles both.
VIM defines kind of quantity as "aspect common to mutually comparable quantities". Hence Brinnel Hardness (653, HBW) and the Rockwell C hardness (60, HRC) are not of the same kind of quantity because they cannot be compared in general, although comparison may be possible for a particular class of material. There is a engineering understanding of the general concept that the Brinnel and Rockwell procedures are intended to measure - i.e. "hardness". This is not a kind of quantity as defined in the VIM, but is a useful concept nonetheless.
A strawman for system of quantities
A strawman UML diagram for 'system of quantities is: 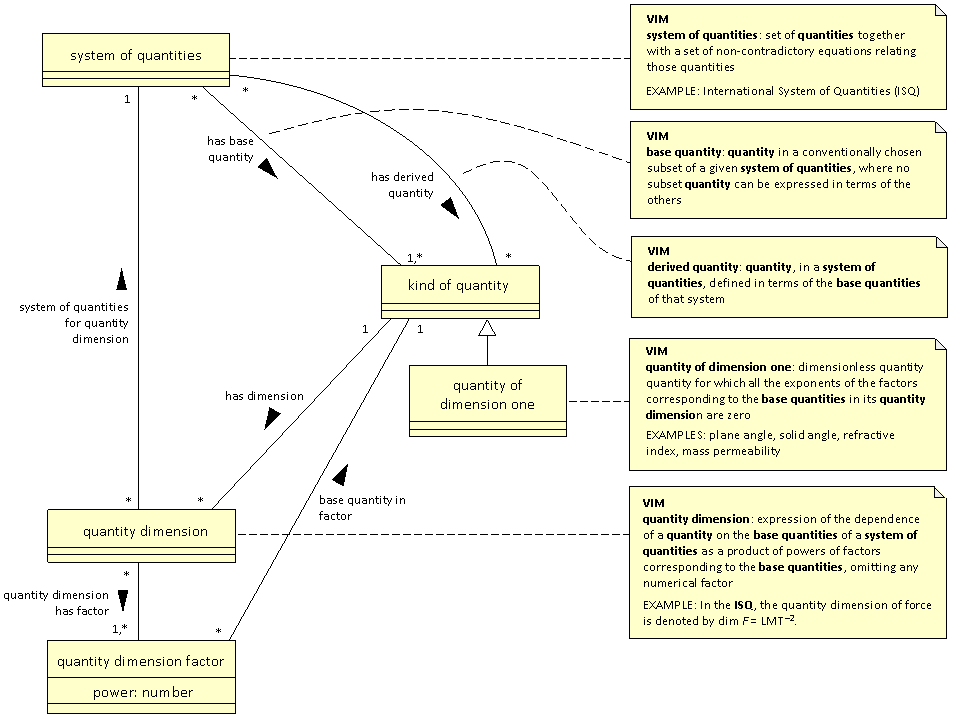
It was pointed out during the discussion that:
- there can be many different systems of quantities, with different base and derived quantities;
- a system of quantities is not the same as a system of units.
Both conclusions are also contained within the VIM. Hence being a base quantity or derived quantity is not a inherent property of a kind of quantity, but a relationship between a kind of quantity and a system of quantities.
A strawman for system of units
The text in the VIM says that a base unit or derived unit for a system of units correspond to a base quantity or derived quantity respectively. The VIM does not say that there is anything special in the way in which a unit is defined that makes it a base unit or derived unit.
A strawman UML diagram for system of units that is analogous to the diagram for system of quantities is: 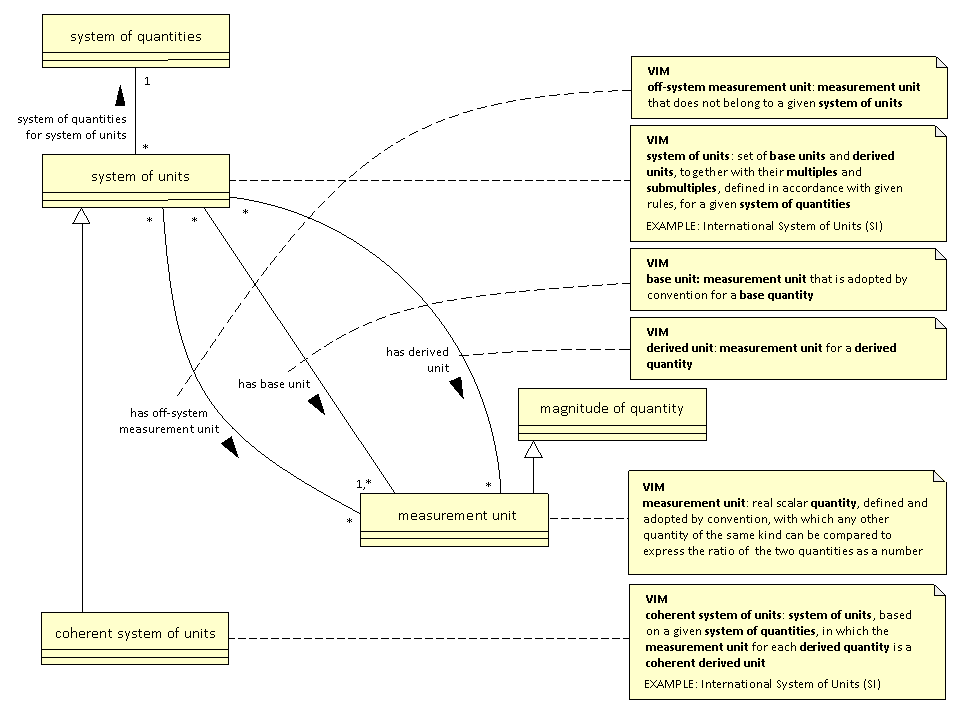
The original UML diagram supplied by Ed contains the text definition "A base unit is defined by a physical phenomenon, i.e., a 'definite description'". Following this approach it is natural to make base unit a subclass of measurement unit. However an "off-system measurement unit" may also be defined by a physical phenomenon. Hence it may be best to add this as: 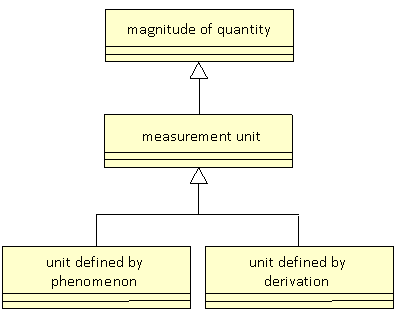
A strawman for scale
The discussion so far has recognised the importance of scales, but has not gone into details. Extracting from the original UML diagram for scales supplied by Ed, and using VIM terminology wherever possible, a strawman UML diagram is: 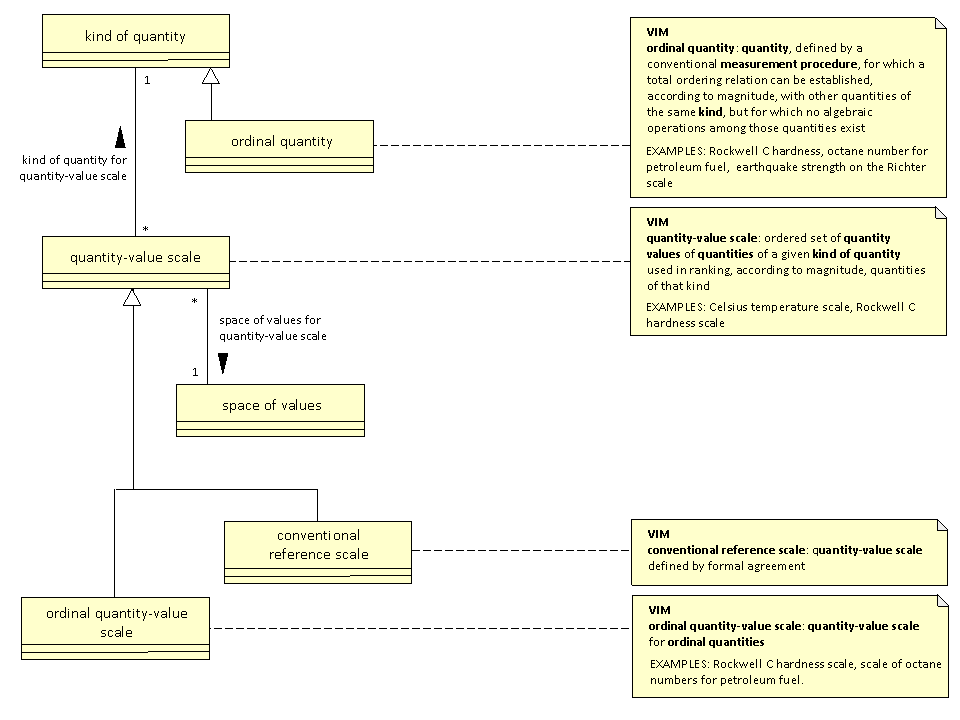
The object space of values has been added. For most scales, this is a real or integer interval, perhaps unbounded. However, it could be something else, such as a sequence of letters "a", "b", "c", etc..
VIM does not give an example of conventional reference scale. Perhaps ITS90 (http://www.bipm.org/en/publications/its-90.html) is such a scale.
The relationship between scales and units has not been addressed in this strawman.
Relationship between the strawman UML model and UnitsML
UnitsML has much important content relevant to symbols, prefixes and units conversion. However the only those parts of UnitsML relevant to the strawman diagrams for quantity, system of quantities, unit, system of units and scale are considered here. Some relationships between objects and relationships in the strawman and elements and attributes in UnitsML are as follows:
- kind of quantity: The object in the strawman corresponds to the element Quantity in UnitsML.
- measurement unit: The object in the strawman broadly corresponds to the element Unit in UnitsML. However, Fahrenheit is regarded as an instance of Unit, whereas in the strawman it would be an instance of scale.
- quantity value: The object in the strawman does not corresponds to an element in UnitsML. Instead the presence of a UnitsML Unit element as a child of an element defined elsewhere represents a reference for quantity value relationship.
- magnitude of quantity: The object in the strawman is outside the scope of UnitsML, except when it is a measurement unit.
- magnitude is within: This relationship between magnitude of quantity and kind of quantity is outside the scope of UnitsML except when the kind of quantity is a measurement unit. In this case, the relationship is provided within UnitsML by the child element QuantityReference of Unit.
- quantity dimension: The object in the strawman corresponds to the element Dimension in UnitsML.
- has dimension: This relationship between kind of quantity and dimension is provided within UnitsML by the attribute dimensionURL of Quantity. UnitsML allows a dimension to be specified for a Unit. In the strawman, this is superfluous because a a measurement unit is of exactly one kind of quantity for which a dimension can be specified.
Relationship between the strawman UML model and The Unified Code for Units of Measure (UCUM)
The UCUM has much important content concerning a formal algebra for the derivation of units. The elements unit and base-unit within the UCUM XML schema corresponds to the object measurement unit in the strawman.
Relationship between the strawman UML model and the MyMobileWeb Measurement Units Ontology (MUO)
The MyMobileWeb has assimulated the UCUM units as instances of a class within a larger ontology. Some relationships between objects and relationships in the strawman and elements and attributes in MUO are as follows:
- kind of quantity: The object in the strawman corresponds to the class PhysicalQuality in the MUO. The MUO is admirably precise in specifying that it is not a particular quantity.
- measurement unit: The object in the strawman broadly corresponds to the class UnitOfMeasurement in the MUO. However, Fahrenheit is regarded as an instance of UnitOfMeasurement, whereas in the strawman it would be an instance of scale.
- quantity value: It is natural to associate this object in the strawman with the class QualityValue in the MUO. This is probably broadly true, but in the MUO QualityValue has the property inTime which specifies when the value occurs. In the strawman, time is more appropriately associated with the particular quantity or with the temporal part of the particular phenomenon body or substance that possesses it.
Relationship between the strawman UML model and the proposed UoM extension to SysML
Clause "C.5 Model Library for Quantities, Units, Dimensions and Values (QUDV)" is a proposed addition to the SysML specification [1]. It is currently being considered by the SysML Revision Task Force (RTF). If accepted, it will become a non-normative annex of the SysML 1.2 specification.
Figure C.8 QUDV Concepts diagram has much the same scope as the strawman UML diagrams. Both are derived from the VIM, and are therefore similar. Some differences are:
- The proposed SysML diagram has a many to many relationship between SystemOfUnits and SystemOfQuantities. The VIM says that a system of units is "defined ... for a given system of quantities". Hence in accordance with the VIM, the strawman UML says that a system of units has a relationship with exactly one system of quantities.
- The proposed SysML diagram has not sought to separate the different concepts within the concept called "quantity" by the VIM.
- The proposed SysML diagram renames "kind of quantity" in the VIM as "QuantityKind". (There is belief in the USA and Germany that nouns can be placed side by side with an implicit relationship. There is a belief in the UK and France that the relationship should be stated explicitly by a preposition. :)
In Figure C.10 QUDV QuantityKind diagram, the class "QuantityKind" has a subclass "DerivedQuantityKind". This is incorrect, because a kind of quantity may be a base quantity in one systems of quantities, but a derived quantity in another. The kind of quantity electric charge is an example of this.
Q1 particular quantity: class of individual quantifiable properties of individual things (the tropes)
Examples: The length of my thumb (and no one else's thumb).
Q2 kind of quantity (as class of particular quantity): class whose members are subclasses of particular quantity in which all the members are comparable
Example: length (as a class of particular quantity). The length of my thumb is a member of length (as a class of particular quantity).
Q3 magnitude of quantity: class whose members are subclasses of particular quantity in which all the members are equal
Note: A member of magnitude of quantity is an equivalence class.
Example: The length magnitude called "5cm", which includes the length of my thumb, the height of my coffee cup, and so on.
Q4 kind of quantity (as class of magnitude): class whose members are subclasses of magnitude of quantity in which all the members are subclasses of the same kind of quantity (as class of particular quantity)
Example: length (as a class of magnitude of quantity). The length magnitude called "5cm" is a member of length (as a class of magnitude of quantity).
Note: measurement unit is a subclass of 'magnitude of quantity. Hence each measurement unit is a member of a kind of quantity (as class of magnitude. The metre is a member of length (as a class of magnitude).
Discussion
The definitions of Q1 to Q4 were proposed by Ed Barkmeyer.
The distinction between Q2 kind of quantity (as class of particular quantity) and Q4 kind of quantity (as class of magnitude) is not made in the strawman UML diagrams. In the UML diagrams there is a relationship magnitude is within beween magnitude of quantity and kind of quantity. The formal meaning of this relationship depends upon the formal definitions, as follows:
- the relationship between magnitude_of_quantity and kind of quantity (as class of particular quantity) is subclass;
- the relationship between magnitude_of_quantity and kind of quantity (as class of magnitude) is member.
An informal explanation of the different "quantity" concepts
The class particular quantity has properties of things as members, as shown in 
The members of particular quantity can be collected into subclasses which are comparable, as shown in 
Each of these subclasses of particular quantity is a kind of quantity (as class of particular quantity, as shown in 
The members of particular quantity can be collected into subclasses which are equal, as shown in 
Each of these subclasses of particular quantity is a magnitude of quantity, as shown in 
The members of magnitude of quantity can be collected into subclasses such that the members of each member are comparable. Each of these subclasses is a kind of quantity (as class of magnitude) as shown in 
Meta-levels of the quantity concepts
The meta-levels of the quantity concepts are illustrated by development of the example provided by Hajo Rijgersberg shown in

The only concrete object is "length of my table at my instant", which is a member of particular quantity. All the others objects are abstractions at different meta-levels. The higher level abstractions may seem unnecessarily complicated, but a justification is as follows:
- "1.3 metres" and "the metre" are both members of magnitude of quantity and of "length as a class of magnitude" (neither are members of "length as a class of particular quantity" because both are abstractions and not members of particular quantity);
- that "1.3 metres" can be expressed in terms of its relationship with a unit, such as "the metre", is a property of the class "length as a class of magnitude";
- a subclass of Q4, kind of quantity as class of magnitude can be defined that contains all members for which a simple relationship with a unit exists.

